Effortlessly Calculate The Slovin Formula
Slovin merupakan salah satu teknik perhitungan ukuran sampel minimum (bukan ukuran sampel mutlak) dalam penelitian kuantitatif tanpa memperhatikan karakteristik populasi. Slovin merupakan teknik yang cenderung sederhana apabila dibandingkan dengan teknik lainnya. Slovin digunakan ketika ukuran populasi akses yang diketahui secara pasti (finite population), juga direkomendasikan digunakan ketika ukuran populasi akses tidak diketahui secara pasti (infinite population), sehingga peneliti bisa memanfaatkan populasi yang lebih general untuk menghitung ukuran sampel minimum. Dengan margin of error (MoE) sebesar 10% maka ukuran sampel menjadi tidak terlalu besar karena peneliti tidak pernah mengetahui ukuran populasi akses yang sesungguhnya. Namun penulis merekomendasikan untuk menggunakan MoE sebesar 10% apabila peneliti mampu memperkirakan kecenderungan populasi aksesnya berjumlah kecil atau sedikit serta sulit diakses, dan peneliti dapat menggunakan MoE sebesar 5% apabila kecenderungan populasi aksesnya berjumlah sangat besar serta mudah diakses.
Tentu saja pemilihan margin of error (MoE) tidak terlepas dari tingkat representasi ukuran sampel terhadap ukuran populasinya, semakin rendah margin of error (MoE) maka semakin representatif ukuran sampel terhadap ukuran populasi. Pernyataan ini bahkan sesuai dengan Teorema Limit Pusat (Central Limit Theorem) yang berbunyi semakin besar ukuran sampel maka semakin representatif atau semakin mendekati normal.
Populasi Target adalah populasi yang lebih luas, diluar populasi akses yang memiliki kondisi yang sejenis, sehingga peneliti memungkinkan melakukan generalisasi.
Populasi Akses adalah populasi yang telah direncanakan dalam penelitian (sesuai dengan sampling frame atau karakteristik (kriteria) populasi) yang tersedia dan dapat dijangkau oleh peneliti. Ukuran populasi target bisa diketahui ataupun bisa tidak diketahui, sehingga peneliti bisa menggunakan populasi akses untuk membantu mempermudah mendapatkan ukuran sampel minimum.
Contoh :
Peneliti ingin meneliti tentang kepuasan mahasiswa wanita semester 6 Arena Institute terhadap penggunaan Macbook.
(Note : Dalam suatu penelitian peneliti sebaiknya menentukan sampling unit dan sampling frame sebelum menentukan populasi dan sampel)
Sampling unit : Individu
Sampling Frame :
1. Mahasiswa berjenis kelamin wanita
2. Kuliah di Arena Institute
3. Sedang menempuh kuliah semester 6
4. Menggunakan Macbook
maka sampling frame ini merupakan kriteria atau karakteristik populasi, sehingga populasi dalam penelitian ini adalah mahasiswa wanita semester 6 Arena Institute yang menggunakan Macbook. Populasi yang seperti ini adalah populasi akses. Sehingga sampel yang diambil sesuai dengan karakteristik dari populasi akses tersebut. Jika kita mengingat definisi sampel adalah sebagian dari populasi, maka karakteristik sampel harus sama dengan karakteristik populasi.
"Sample Characteristics = Population Characteristics"
Sementara populasi targetnya siapa..??
Jika kita memperhatikan sampling frame, informasi mengenai jumlah mahasiswa wanita yang sedang menempuh kuliah semester 6 yang menggunakan Macbook di Arena Institute, Arena University, Sekolah Tinggi Statistika Arena. maka karakteristik yang seperti ini disebut dengan populasi target. mahasiswa mahasiswa wanita yang sedang menempuh kuliah semester 6 yang menggunakan Macbook di Arena Institute memiliki kesamaan karakteristik dengan mahasiswa wanita yang sedang menempuh kuliah semester 6 yang menggunakan Macbook yang ada di Arena University dan Sekolah Tinggi Statistika Arena. Sehingga pada penelitian berikutnya populasi ini memungkinkan menjadi populasi akses (karena memiliki karakteristik yang sejenis)
Dari contoh ini, apakah peneliti bisa memastikan jumlah mahasiswa wanita Arena Institute yang menggunakan Macbook?? tentu saja tidak.! sehingga peneliti bisa menggunakan populasi yang lebih general untuk mendapatkan ukuran sampel minimum, yaitu wanita yang sedang menempuh kuliah semester 6 di Arena Institute.
Formula slovin adalah sebagai berikut :
by : Danny Prasetyo Hartanto (2023)
Using The InQuest Calculator
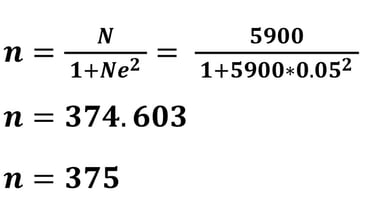
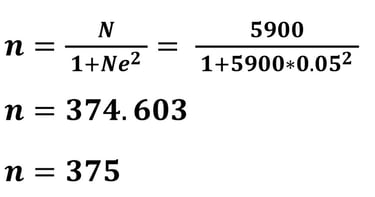
Apabila kita memperhatikan ukuran sampel minimum dengan MoE sebesar 5% jauh lebih tinggi daripada menggunakan MoE sebesar 10%. Coba kita evaluasi.! apakah dengan sampel minimum 375 peneliti bisa mendapatkannya semua? Mungkin akan sulit didapatkan, maka untuk mempermudah penelitian (sesuai prinsip parsimony) maka sebaiknya peneliti menggunakan MoE sebesar 10% sehingga diperoleh ukuran sampel yang tidak terlalu tinggi.
Untuk mempermudah menghitung formula slovin, peneliti dapat mengakses InQuest Calculator berikut :
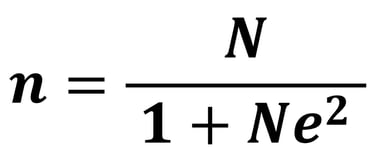
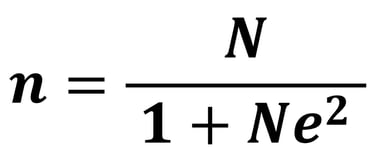
Keterangan :
N = ukuran populasi
n = ukuran sampel
e = Batas toleransi kesalahan atau Margin of Error
Simulasi 1
Untuk simulasi formula slovin, kita gunakan contoh yang sudah ada.
Misalkan ukuran populasi yang lebih general sebesar 5900, maka ukuran sampel minimum menggunakan formula slovin adalah sebagai berikut :
Apabila peneliti menggunakan error (MoE) sebesar 5% (0.05), maka perhitungan ukuran sampel minimum adalah
Apabila peneliti menggunakan error (MoE) sebesar 10% (0.1), maka perhitungan ukuran sampel minimum adalah
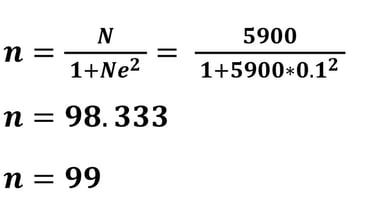
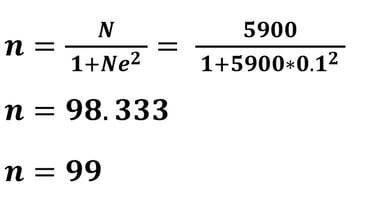
Alternative Inquest Calculator
Main Inquest Calculator
Pembulatan dalam Ukuran Sampel
Apabila kita mencermati hasil ukuran sampel dengan MoE 5% diperoleh 347.603 dibulatkan menjadi 348, sementara ukuran sampel dengan MoE 10% diperoleh 98.333 dibulatkan menjadi 99. Mengapa semua dibulatkan keatas?
Bukankah secara teori jika desimal ≥ 0.5 seharusnya dibulatkan keatas menjadi 1, dan < 0.5 dibulatkan kebawah menjadi 0?
Teori tersebut memang benar, namun dalam kasus sampel teori ini tidak berlaku. Mengapa?
Alasan 1. Populasi dan sampel terkait dengan sampling unit, bisa individu, bisa organisasi, wilayah, dsb. Kita bayangkan 0.2 individu apakah kita meminta pendapat pada sebagian tubuh manusia, misalkan tangan saja atau kepala saja? tentu tidak masuk akal, maka kita meminta pendapat tubuh yang utuh, sehingga meneliti 0.2 individu sama halnya meneliti 1 individu.
Alasan 2. Kembali pada Teorema Limit Pusat (Central Limit Theorem) bahwa semakin besar ukuran sampel maka semakin representatif atau semakin mendekati normal, sehingga apabila peneliti membulatkan kebawah maka sampel menjadi 98 sehingga diperoleh MoE sebesar 10.017%, sedangkan apabila peneliti membulatkan keatas maka sampel menjadi 99 sehingga diperoleh MoE sebesar 9.966%.
MoE yang diperoleh ketika peneliti membulatkan keatas tentu lebih rendah dibandingkan ketika peneliti membulatkan kebawah, sehingga dengan membulatkan keatas peneliti bisa menggunakan ukuran sampel yang lebih representatif. Dengan demikian,
"Pembulatan dalam ukuran sampel adalah pembulatan keatas"
Untuk menghitung margin of error (MoE) dari Slovin bisa menggunakan calculator berikut :
Referensi :
Cochran, W.G. 1977. Sampling Technique. New York : John Wiley and Sons. Inc
Kish, L. 1965. Survey Sampling. New York : John Wiley and Sons, Inc
Machali, I. 2015. Statistik Manajemen Pendidikan, Teori dan Praktik Statistik dalam bidang pendidikan, Penelitian, Ekonomi Bisnis, dan Ilmu-Ilmu Sosial Lainnya. Yogyakarta : Kaukaba Dipantara
Pitard, F.F. 2019. Theory of Sampling and Sampling Practice. Washington D.C. : Chapman and Hall/CRC
Rao, P.S.R.S. 2000. Sampling Methodologies with Applications. Washington D.C. : Chapman and Hall/CRC
Scheaffer, R.L., W. Mendenhall, W. and L. Ott. 1990. Elementary Survey Sampling. 4th Edition. Boston : PWS-KENT Publishing Company
Slovin. 1960. Slovin's formula for sampling technique. New York: Simon dan Schuster Inc
Solimun, Fernandes, A.A.R., Nurjannah. 2017. Metode Statistika Multivariat Pemodelan Persamaan Struktural (SEM) Pendekatan WarpPLS. Malang : UB Press
Walpole, R.E. 1995. Pengantar Statistika, Edisi ke-3, Jakarta : Gramedia Pustaka Utama.
Wardhani, N.W.S., Nugroho, W.H., Lusia, dan D.W., Rahmi. 2021. Teknik Sampling dan Survey (Konsep Dasar dan Aplikasi). Malang : UB Press
 - versi 2 White-AMqzvNxKRPfRLVOA.png)