 - versi 2 White-AMqzvNxKRPfRLVOA.png)
The Pearson's Correlation Table
"r Table"
by : Danny Prasetyo Hartanto (2024)
The Pearson's Correlation Table atau r Tabel merupakan pembanding bagi koefisien korelasi pearson (statistik uji r atau r statistic atau peneliti suka menyebut dengan r hitung) pada saat pengambilan keputusan dalam pengujian hipotesis pada analisis Korelasi Pearson
Statistika (teknik analisis data) yang menggunakan statistik uji r adalah analisis Korelasi Pearson dan Analisis Korelasi Point Biserial (Pendekatan Korelasi Pearson)
Kritera pengujian atau kriteria pengambilan keputusan yang menggunakan statistik uji r adalah sebagai berikut :
Apabila koefisien korelasi pearson (statistik uji r / r statistic / r hitung) bernilai positif maka kriteria pengujian sebagai berikut
r statistic ≥ r table (alpha, df)
maka H0 ditolak
Apabila koefisien korelasi pearson (statistik uji r / r statistic / r hitung) bernilai negatif maka kriteria pengujian sebagai berikut
-r statistic ≤ -r table (alpha, df)
maka H0 ditolak
Kedua kriteria pengujian tersebut dapat disederhanakan menjadi bentuk general yaitu dengan mengabsolutkan atau memutlakkan (hasil absolut atau mutlak adalah positif) koefisien korelasi pearson (statistik uji r / r statistic / r hitung). Kriteria yang seperti ini dapat berlaku pada koefisien korelasi pearson (statistik uji r / r statistic / r hitung) dengan mengabaikan tanda positif atau negatif.
|r statistic| ≥ |r table| (alpha, df)
maka H0 ditolak
Besarnya degree of freedom (df) dalam analisis korelasi pearson adalah
df = n - 2
dimana : n = besar sampel (observasi)
Untuk mendapatkan skor r tabel secara mudah dan instan, peneliti dapat mengakses InQuest Calculator R tabel berikut :
|r statistic| ≥ |r table| (alpha, df) maka dinyatakan Signifikan (H0 ditolak)
Untuk mendapatkan skor r tabel secara manual, peneliti dapat menggunakan r tabel berikut
Klik shortcut sesuai dengan sampel (n) atau degree of freedom (df) yang anda butuhkan
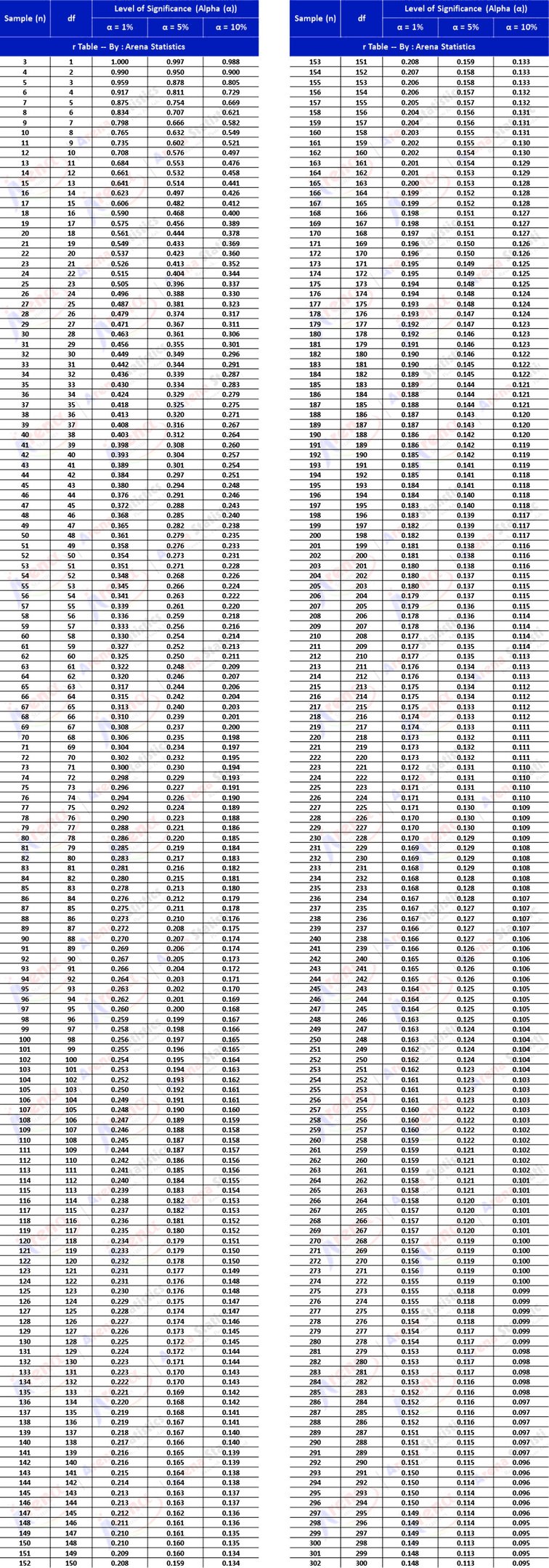
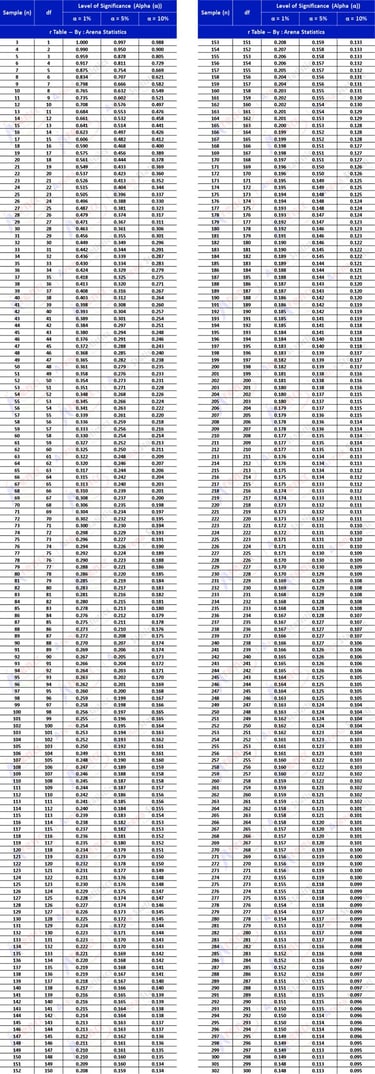
r Tabel dengan sampel (n) 3 - 302 atau Degree of Freedom (df) 1 - 300
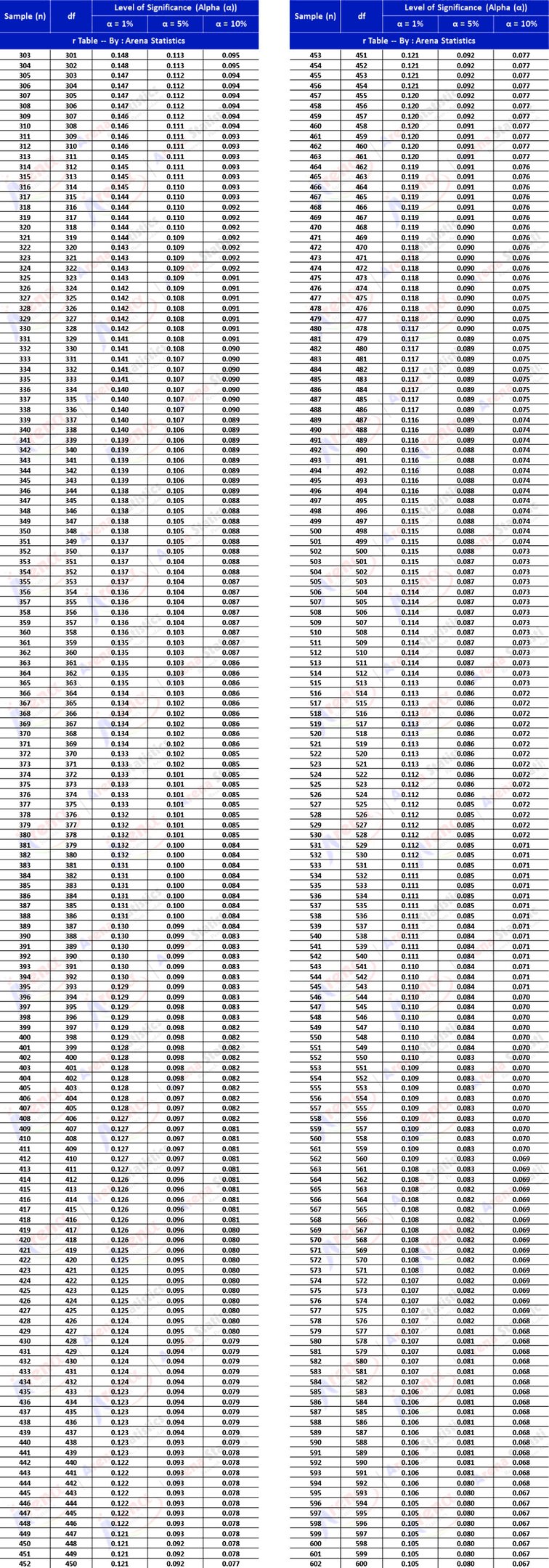
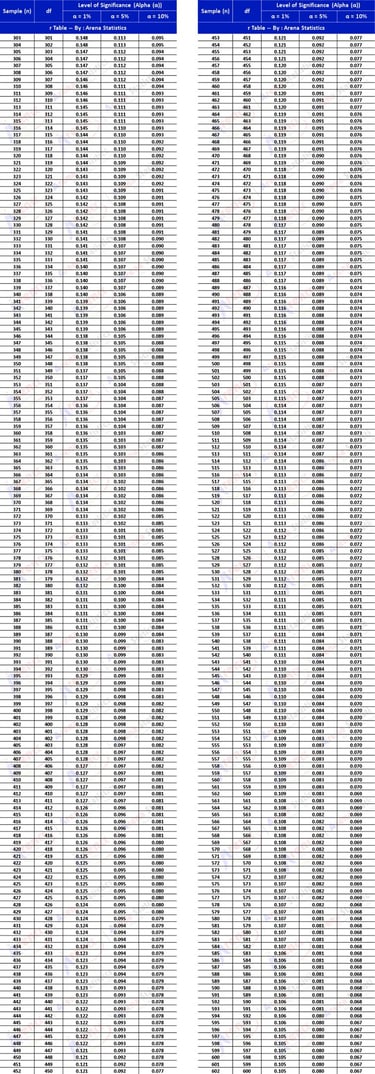
r Tabel dengan sampel (n) 303 - 602 atau Degree of Freedom (df) 301 - 600
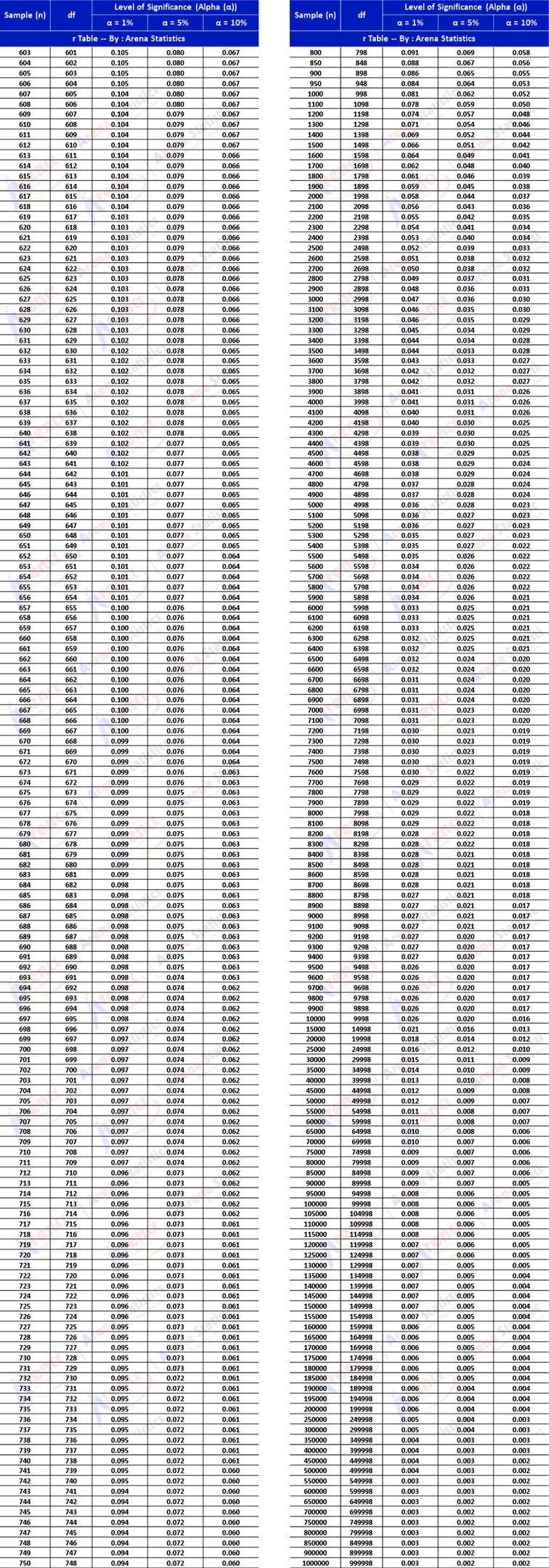
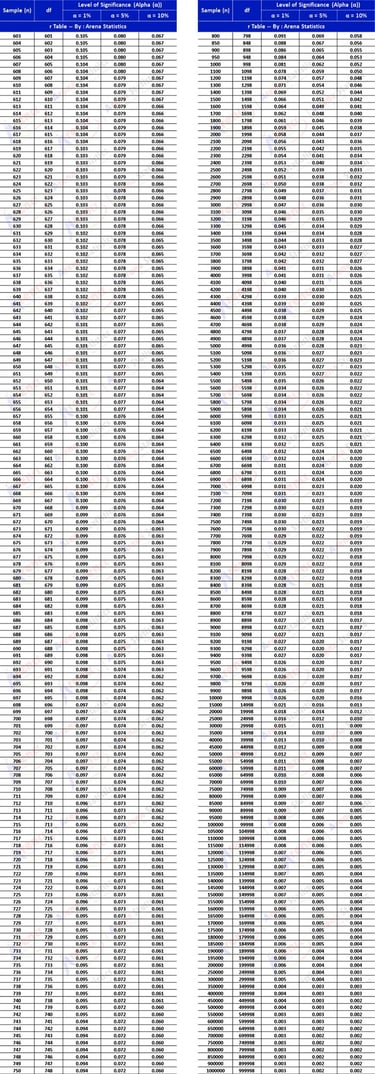
r Tabel dengan sampel (n) 603 - Infinite atau Degree of Freedom (df) 601 - Infinite
Chi Squared Distribution (distribusi Khai Kuadrat) atau Chi Square Tabel (tabel Khai Kuadrat) merupakan pembanding bagi statistik uji chi square (chi square statistic atau biasa disebut dengan chi square hitung) pada saat pengambilan keputusan dalam pengujian hipotesis pada statistika inferensial.
Statistika (teknik analisis data / statistika inferensial) yang menggunakan statistik uji chi square diantaranya
Statistika Komparatif (Uji Beda)
Pengujian signifikansi Mc Nemar, Kruskal Walis, Median, Friedman, Kendall's W, dsb
Analisis Korelasi
Pengujian signifikansi Korelasi Chi Square dan Contingency Coefficient
Analisis Regresi
Pengujian signifikansi parsial (Wald) dalam regresi logistik, pengujian signifikansi simultan (Omnibus Test) dalam regresi logistik, pengujian kelayakan model (Hosmer & Lemeshow Test) dalam regresi logistik, pengujian asumsi normalitas, pengujian asumsi heteroskedastisitas menggunakan teknik lagrange multiplier, pengujian asumsi autokorelasi menggunakan teknik lagrange multiplier, pengujian asumsi linieritas menggunakan teknik lagrange multiplier, dan regresi lainnya
Analisis Data Panel
Chow Test dan Hausman Test dalam regresi data panel, dsb
Analisis Structural Equation Modelling
Goodness of fit dalam Structural Equation Modelling (SEM), dam Partial Least Square (SEM-PLS / biasa disebut PLS)
Referensi :
[1] Pearson, E. S., and Hartley, H. O. 1966. Biometrika Tables for Statisticians Vol. I, 3. XVI + 264 S. Preis 35 s. Auflage. Cambridge :
University Press.
[2] Gujarati, D.N. and Porter, D.C. 1978. Basic Econometrics. Boston: McGraw-Hill
[3] Gujarati, D.N. 2003. Basic Econometrics. Boston: McGraw-Hill
[4] Lehmann, E. L. 1986. Testing Statistical Hypostheses. New York : John Wiley & Sons.
[5] Walpole, R.E. 1995. Pengantar Statistika, Edisi ke-3, Jakarta : Gramedia Pustaka Utama.
[6] Draper, NR and Smith.1992. Analisis Regresi Terapan, edisi kedua. Jakarta : Gramedia Pustaka Utama.
[7] Myers, RH,.1990. Classical and Modern Regression With Aplications. United States of America : PWS-KENT Publishing Company.
[8] Mendenhall, Scheaffer and Wackery. 1981. Mathematical Statistic with application. Boston : Duxbury
[9] Douglas, L, Marchal, W, and Wathen, S. 2006. Basic Statistic for Business and Economics 5th Edition. San Fransiso : Mcgreaw-Hill
International Book Company.
[10] Neave, H.R. 1978. Statistics Tables for Mathematicians, Engineers, Economists, and The Behavioural and Management Sciences.
London : George Allen & Unwin Publisher.