LM Statistic in Autocorrelation Analysis
Asumsi Autokorelasi merupakan salah satu pengujian asumsi klasik dalam analisis regresi (regresi linier, regresi dummy, regresi panel, dsb) yang digunakan untuk menguji hubungan antar series residual yang dihasilkan dari analisis regresi tersebut. Asumsi autokorelasi khusus digunakan pada analisis regresi dengan data time series atau data panel.
Teknik pengujian asumsi autokorelasi yang paling umum digunakan adalah Durbin Watson yang mana menguji hubungan antar series residual pada tingkat pertama (first order). Namun apabila hasil durbin watson tidak memberikan hasil yang memadai dalam pengambilan keputusan, maka peneliti bisa menggunakan teknik alternatif seperti Lagrange Multiplier Test atau Breusch-Godfrey Test.
Lagrange Multiplier Test atau Breusch-Godfrey Test dinilai lebih fleksibel karena dapat menguji adanya masalah autokorelasi pada derajat tinggi, yaitu diasumsikan mengikuti high order autoregressive scheme.
Konsep Lagrange Multiplier Test (LM Test) adalah meregresikan variabel independen dan time lagged residual (residual pada periode sebelumnya) terhadap residual periode saat ini, sebagaimana ditunjukkan persamaan berikut :
by : Danny Prasetyo Hartanto (2025)
Using The InQuest Calculator
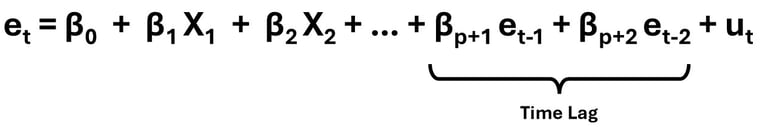
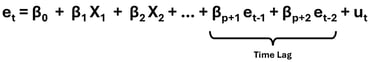
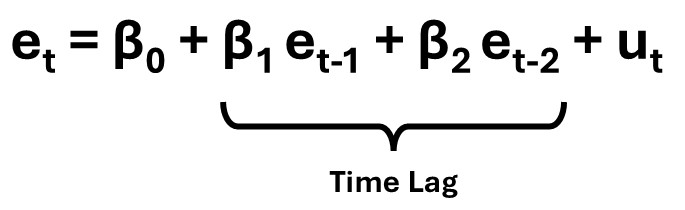
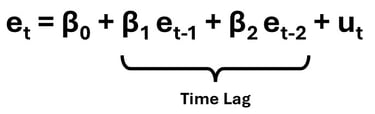
Sedangkan konsep Lagrange Multiplier Test (LM Test) adalah meregresikan time lagged residual (residual pada periode sebelumnya) terhadap residual periode saat ini, sebagaimana ditunjukkan persamaan berikut :
Hipotesis pengujian Asumsi Autokorelasi :
H0 : Tidak terjadi Autokorelasi antar series residual
H1 : Terjadi Autokorelasi antar series residual
Formula LM statistic :
LM statistic = n * Rsquare
Formula tersebut juga bisa juga ditulis
Chi Sq statistic = n * Rsquare
Keterangan :
n = observasi
Rsquare = Koefisien Determinasi Analisis Regresi
Kriteria pengujian LM Statistic adalah sebagai berikut
LM statistic < Chi Sq table (alpha, df)
atau bisa juga ditulis
Chi Sq statistic < Chi Sq table (alpha, df)
maka H0 diterima,
yang berarti tidak terjadi autokorelasi antar series residual.
Besarnya degree of freedom (df) yang digunakan untuk menentukan chi square tabel dalam pengujian asumsi autokorelasi adalah
df = banyaknya time lag yang masuk dalam model regresi
Contoh hasil pengujian asumsi autokorelasi menggunakan Lagrange Multiplier Test
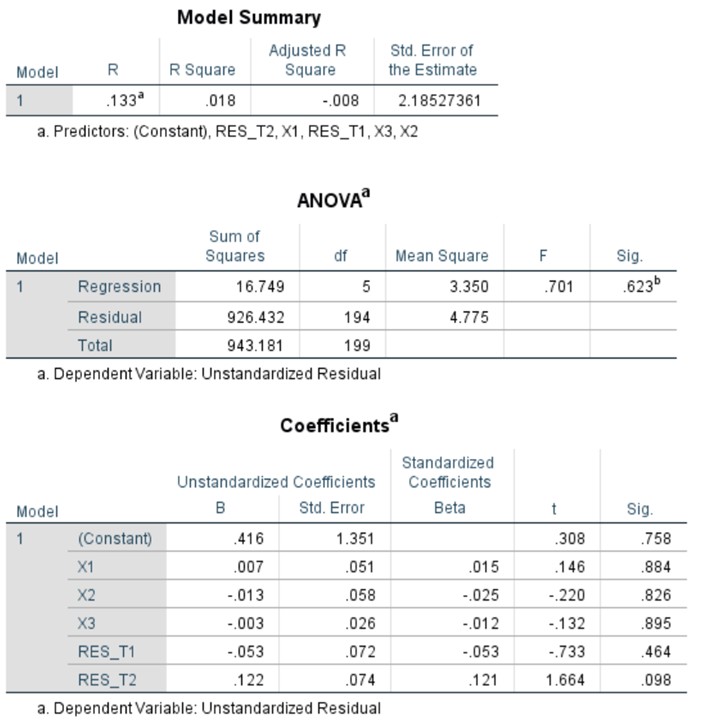
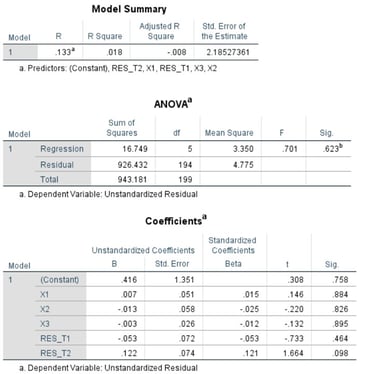
Untuk mendapatkan LM statistic, maka peneliti perlu menghitung secara manual, sebagaimana berikut
LM statistic = n * Rsquare
LM statistic = 200 * 0.018
LM statistic = 3.600
di sisi lain,
Chi Sq tabel = Chi Sq (alpha, df)
Chi Sq tabel = Chi sq (0.05, 2)
Chi Sq tabel = 5.992
Hasil perhitungan tersebut diketahui LM statistic < Chi Sq tabel. Oleh karena itu tidak terjadi autokorelasi antar series residual
Contoh hasil pengujian asumsi autokorelasi menggunakan Breusch Godfrey Test
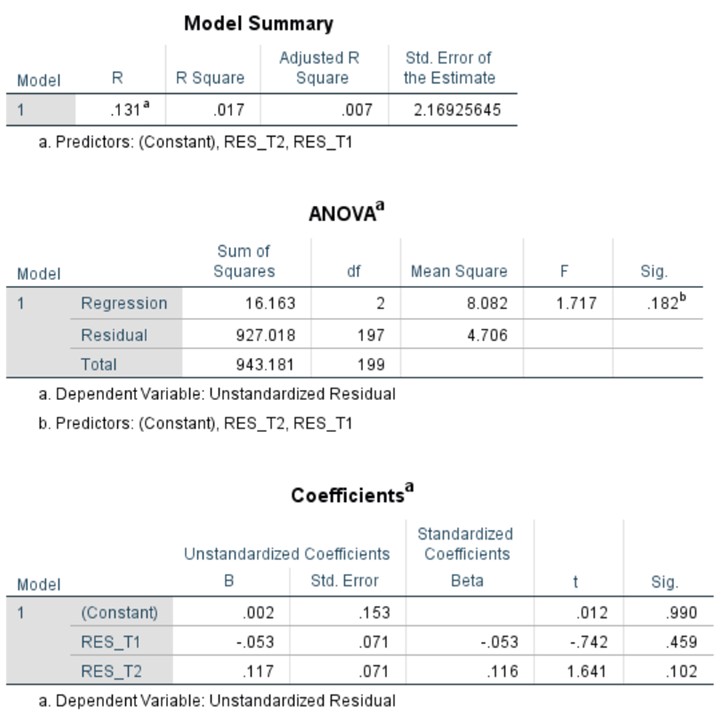
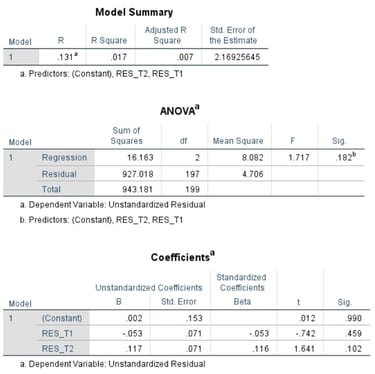
Untuk mendapatkan LM statistic, maka peneliti perlu menghitung secara manual, sebagaimana berikut
LM statistic = n * Rsquare
LM statistic = 200 * 0.017
LM statistic = 3.400
di sisi lain,
Chi Sq tabel = Chi Sq (alpha, df)
Chi Sq tabel = Chi sq (0.05, 2)
Chi Sq tabel = 5.992
Hasil perhitungan tersebut diketahui LM statistic < Chi Sq tabel. Oleh karena itu tidak terjadi autokorelasi antar series residual
Untuk mempermudah menghitung LM statistic pada asumsi autokorelasi, peneliti dapat mengakses InQuest Calculator berikut :
Untuk mempermudah menghitung LM statistic pada asumsi autokorelasi, peneliti dapat mengakses InQuest Calculator berikut :
Referensi :
Draper, NR and Smith. 1998. Applied Regression Analysis. John Wiley & Sons.
Davidson, R., and J. G. MacKinnon. 1993. Estimation and Inference in Econometrics. New York: Oxford University Press.
Durbin, J., and G. S. Watson. 1950. Testing for serial correlation in least squares regression. I. Biometrika 37: 409-428.
Efendi, A., Wardhani, N.W.S., Fitriani, R., dan Sumarminingshih, E. 2020. Analisis Regresi Teori dan Aplikasi dengan R. Malang : UB Press
Engle. R. F. 1982a. A General Approach to Lagrange Multiplier Model Diagnostics. Journal of Econometrics. 20:83-104.
EViews 12 User’s Guide II. 2020. California : IHS Markit - EViews (https://cdn1.eviews.com/EViews%2012%20Users%20Guide%20II.pdf)
Fitriani, R., Nurjannah, Pusdiktasari, Z.F. 2021. Dasar-Dasar Ekonometrika dan Terapannya dengan Gretl. Malang : UB Press
Gujarati, D.N. and Porter, D.C. 1978. Basic Econometrics. Boston: McGraw-Hill.
Gujarati, D.N. 2003. Basic Econometrics. Boston: McGraw-Hill.
Myers, RH. 1990. Classical and Modern Regression With Aplications. United States of America : PWS-KENT Publishing Company.
Neave, H.R. 1978.Statistics Tables for Mathematicians, Engineers, Economists, and The Behavioural and Management Sciences.London : George Allen & Unwin Publisher.
Suliyanto. 2011. Ekonometrika Terapan : Teori & Aplikasi dengan SPSS. Yogyakarta : Andi Offset
W. Krämer & H. Sonnberger (1986), The Linear Regression Model under Test. Heidelberg: Physica
Weisberg, S. 2005. Applied Linier Regression, 3th Edition. New Jersey : John Wiley & Sons.
 - versi 2 White-AMqzvNxKRPfRLVOA.png)